COMPUTADORA
Máquina capaz de efectuar una secuencia de
operaciones mediante un
programa, de tal manera, que se realice un procesamiento sobre un conjunto de
datos de entrada, obteniéndose otro conjunto de datos de salida.
TIPOS DE COMPUTADORAS
Se clasifican de acuerdo al principio de operación de Analógicas y Digitales.
COMPUTADORA ANALÓGICA
Aprovechando el hecho de que diferentes fenómenos físicos se describen por relaciones
matemáticas similares (v.g. Exponenciales, Logarítmicas, etc.) pueden entregar la solución muy rápidamente. Pero tienen el inconveniente que al cambiar el problema a resolver, hay que realambrar la circuitería (cambiar el
Hardware).
COMPUTADORA DIGITAL
Están basadas en dispositivos biestables, i.e., que sólo pueden tomar uno de dos
valores posibles: ‘1’ ó ‘0’. Tienen como ventaja, el
poder ejecutar diferentes
programas para diferentes
problemas, sin tener que la necesidad de modificar físicamente la máquina.
HISTORIA DE LA COMPUTACIÓN
Uno de los primeros dispositivos mecánicos para contar fue el
ábaco, cuya
historia se remonta a las antiguas civilizaciones griega y romana. Este dispositivo es muy sencillo, consta de
cuentas ensartadas en varillas que a su vez están montadas en un marco rectangular. Al desplazar las cuentas sobre varillas, sus posiciones representan valores almacenados, y es mediante dichas posiciones que este representa y almacena datos. A este dispositivo no se le puede llamar
computadora por carecer del elemento fundamental llamado programa.
Otro de los
inventos mecánicos fue la Pascalina inventada por Blaise
Pascal (1623 - 1662) de
Francia y la de Gottfried Wilhelm von Leibniz (1646 - 1716) de
Alemania. Con estas
máquinas, los datos se representaban mediante las posiciones de los engranajes, y los datos se introducían manualmente estableciendo dichas posiciones finales de las ruedas, de manera similar a como leemos los números en el cuentakilómetros de un automóvil.
La primera computadora fue la máquina analítica creada por Charles Babbage,
profesor matemático de la
Universidad de Cambridge en el siglo XIX. La idea que tuvo Charles Babbage sobre un
computador nació debido a que la elaboración de las tablas matemáticas era un
proceso tedioso y propenso a errores. En 1823 el
gobierno Británico lo apoyo para crear el
proyecto de una máquina de diferencias, un dispositivo mecánico para efectuar sumas repetidas.
Mientras tanto Charles Jacquard (francés), fabricante de
tejidos, había creado un telar que podía reproducir automáticamente patrones de tejidos leyendo la
información codificada en patrones de agujeros perforados en
tarjetas de papel rígido. Al enterarse de este
método Babbage abandonó la máquina de diferencias y se dedico al proyecto de la máquina analítica que se pudiera programar con tarjetas perforadas para efectuar cualquier
cálculo con una precisión de 20 dígitos. La
tecnología de la época no bastaba para hacer realidad sus ideas.
El mundo no estaba listo, y no lo estaría por cien años más.
En 1944 se construyó en la Universidad de Harvard, la Mark I, diseñada por un equipo encabezado por Howard H. Aiken. Esta máquina no está considerada como computadora
electrónica debido a que no era de propósito general y su funcionamiento estaba basado en dispositivos electromecánicos llamados relevadores.
En 1947 se construyó en la Universidad de Pennsylvania la ENIAC (Electronic Numerical Integrator And Calculator) que fue la primera computadora electrónica, el equipo de
diseño lo encabezaron los ingenieros John Mauchly y John Eckert. Esta máquina ocupaba todo un sótano de la Universidad, tenía más de 18 000 tubos de vacío, consumía 200 KW de energía eléctrica y requería todo un
sistema de
aire acondicionado, pero tenía la capacidad de realizar cinco mil operaciones aritméticas en un segundo.
El proyecto, auspiciado por el departamento de Defensa de los
Estados Unidos, culminó dos años después, cuando se integró a ese equipo el ingeniero y matemático húngaro John
von Neumann (1903 - 1957). Las ideas de von Neumann resultaron tan fundamentales para su
desarrollo posterior, que es considerado el padre de las
computadoras.
La EDVAC (Electronic Discrete Variable Automatic Computer) fue diseñada por este nuevo equipo. Tenía aproximadamente cuatro mil bulbos y usaba un tipo de
memoria basado en tubos llenos de
mercurio por donde circulaban
señales eléctricas sujetas a retardos.
La idea fundamental de von Neumann fue: permitir que en
la memoria coexistan datos con instrucciones, para que entonces
la computadora pueda ser programada en un
lenguaje, y no por medio de alambres que eléctricamente interconectaban varias secciones de
control, como en la ENIAC.
Todo este desarrollo de las computadoras suele divisarse por generaciones y el criterio que se determinó para determinar el
cambio de generación no está muy bien definido, pero resulta aparente que deben cumplirse al menos los siguientes requisitos:
La forma en que están construidas.
Forma en que el ser humano se comunica con ellas.
Primera Generación
En esta generación había una gran desconocimiento de las capacidades de las computadoras, puesto que se realizó un estudio en esta época que determinó que con veinte computadoras se saturaría el
mercado de los Estados Unidos en el campo de procesamiento de datos.
Esta generación abarco la década de los cincuenta. Y se conoce como la primera generación. Estas máquinas tenían las siguientes características:
Estas máquinas estaban construidas por medio de tubos de vacío.
Eran programadas en lenguaje de máquina.
En esta generación las máquinas son grandes y costosas (de un
costo aproximado de ciento de miles de dólares).
En 1951 aparece la UNIVAC (NIVersAl Computer), fue la primera computadora comercial, que disponía de mil palabras de memoria central y podían leer cintas magnéticas, se utilizó para procesar el censo de 1950 en los Estados Unidos.
En las dos primeras generaciones, las unidades de entrada utilizaban tarjetas perforadas, retomadas por Herman Hollerith (1860 - 1929), quien además fundó una compañía que con el paso del
tiempo se conocería como IBM (International Bussines Machines).
Después se desarrolló por IBM la IBM 701 de la cual se entregaron 18 unidades entre 1953 y 1957.
Posteriormente, la compañía Remington Rand fabricó el
modelo 1103, que competía con la 701 en el campo científico, por lo que la IBM desarrollo la 702, la cual presentó problemas en memoria, debido a esto no duró en el mercado.
La computadora más exitosa de la primera generación fue la IBM 650, de la cual se produjeron varios cientos. Esta computadora que usaba un esquema de memoria secundaria llamado tambor magnético, que es el antecesor de los discos actuales.
Otros
modelos de computadora que se pueden situar en los inicios de la segunda generación son: la UNIVAC 80 y 90, las IBM 704 y 709, Burroughs 220 y UNIVAC 1105.
Segunda Generación
Cerca de la década de 1960, las computadoras seguían evolucionando, se reducía su tamaño y crecía su capacidad de procesamiento. También en esta época se empezó a definir la forma de comunicarse con las computadoras, que recibía el nombre de
programación de
sistemas.
Las características de la segunda generación son las siguientes:
Se programan en nuevos lenguajes llamados lenguajes de alto nivel.
En esta generación las computadoras se reducen de tamaño y son de menor costo. Aparecen muchas compañías y las computadoras eran bastante avanzadas para su época como la serie 5000 de Burroughs y la ATLAS de la Universidad de Manchester.
Algunas de estas computadoras se programaban con cintas perforadas y otras más por medio de cableado en un tablero. Los programas eran hechos a la medida por un equipo de expertos: analistas, diseñadores, programadores y operadores que se manejaban como una orquesta para resolver los problemas y cálculos solicitados por
la administración. El usuario final de la información no tenía contacto directo con las computadoras. Esta situación en un principio se produjo en las primeras computadoras personales, pues se requería saberlas "programar" (alimentarle instrucciones) para obtener resultados; por lo tanto su uso estaba limitado a aquellos audaces pioneros que gustaran de pasar un buen número de horas escribiendo instrucciones, "corriendo" el programa resultante y verificando y corrigiendo los errores o bugs que aparecieran. Además, para no perder el "programa" resultante había que "guardarlo" (almacenarlo) en una grabadora de astte, pues en esa época no había discos flexibles y mucho menos
discos duros para las PC; este
procedimiento podía tomar de 10 a 45 minutos, según el programa. El panorama se modificó totalmente con la aparición de las computadoras personales con mejore circuitos, más memoria, unidades de disco flexible y sobre todo con la aparición de programas de aplicación general en donde el usuario compra el programa y se pone a trabajar. Aparecen los programas
procesadores de palabras como el célebre
Word Star, la impresionante hoja de cálculo (spreadsheet) Visicalc y otros más que de la noche a la mañana cambian la
imagen de la PC. El sortware empieza a tratar de alcanzar el paso del hardware. Pero aquí aparece un nuevo elemento: el usuario.
El usuario de las computadoras va cambiando y evolucionando con el tiempo. De estar totalmente desconectado a ellas en las máquinas grandes pasa la PC a ser pieza clave en el diseño tanto del hardware como del
software. Aparece el
concepto de human interface que es la relación entre el usuario y su computadora. Se habla entonces de hardware ergonómico (adaptado a las dimensiones humanas para reducir el cansancio), diseños de pantallas antirreflejos y teclados que descansen la muñeca. Con respecto al software se inicia una verdadera carrera para encontrar la manera en que el usuario pase menos tiempo capacitándose y entrenándose y más tiempo produciendo. Se ponen al alcance programas con menús (listas de opciones) que orientan en todo momento al usuario (con el consiguiente aburrimiento de los usuarios expertos); otros programas ofrecen toda una artillería de teclas de control y teclas de
funciones (atajos) para efectuar toda suerte de efectos en
el trabajo (con la consiguiente desorientación de los usuarios novatos). Se ofrecen un sinnúmero de cursos prometiendo que en pocas semanas hacen de cualquier
persona un experto en los programas comerciales. Pero el problema "constante" es que ninguna solución para el uso de los programas es "constante". Cada nuevo programa requiere aprender nuevos controles, nuevos trucos, nuevos menús. Se empieza a sentir que la relación usuario-PC no está acorde con los desarrollos del equipo y de la
potencia de los programas. Hace falta una relación amistosa entre el usuario y la PC.
Las computadoras de esta generación fueron: la Philco 212 (esta compañía se retiró del mercado en 1964) y la UNIVAC M460, la Control Data Corporation modelo 1604, seguida por la serie 3000, la IBM mejoró la 709 y sacó al mercado la 7090, la National Cash Register empezó a producir máquinas para proceso de datos de tipo comercial, introdujo el modelo NCR 315.
La
Radio Corporation of America introdujo el modelo 501, que manejaba
el lenguaje COBOL, para
procesos administrativos y comerciales. Después salió al mercado la RCA 601.
Tercera generación
Con los progresos de la electrónica y los avances de
comunicación con las computadoras en la década de los 1960, surge la tercera generación de las computadoras. Se inaugura con la IBM 360 en abril de 1964.3
Las características de esta generación fueron las siguientes:
Su fabricación electrónica esta basada en circuitos integrados.
Su manejo es por medio de los lenguajes de control de los sistemas operativos.
La IBM produce la serie 360 con los modelos 20, 22, 30, 40, 50, 65, 67, 75, 85, 90, 195 que utilizaban
técnicas especiales del
procesador, unidades de cinta de nueve canales, paquetes de discos magnéticos y otras características que ahora son estándares (no todos los modelos usaban estas técnicas, sino que estaba dividido por aplicaciones).
El
sistema operativo de la serie 360, se llamó OS que contaba con varias configuraciones, incluía un conjunto de técnicas de manejo de memoria y del procesador que pronto se convirtieron en estándares.
En 1964 CDC introdujo la serie 6000 con la computadora 6600 que se consideró durante algunos años como la más rápida.
En la década de 1970, la IBM produce la serie 370 (modelos 115, 125, 135, 145, 158, 168). UNIVAC compite son los modelos 1108 y 1110, máquinas en gran
escala; mientras que CDC produce su serie 7000 con el modelo 7600. Estas computadoras se caracterizan por ser muy potentes y veloces.
A finales de esta década la IBM de su serie 370 produce los modelos 3031, 3033, 4341. Burroughs con su serie 6000 produce los modelos 6500 y 6700 de avanzado diseño, que se reemplazaron por su serie 7000. Honey - Well participa con su computadora DPS con varios modelos.
A mediados de la década de 1970, aparecen en el mercado las computadoras de tamaño mediano, o minicomputadoras que no son tan costosas como las grandes (llamadas también como mainframes que significa también, gran sistema), pero disponen de gran capacidad de procesamiento. Algunas minicomputadoras fueron las siguientes: la PDP - 8 y la PDP - 11 de Digital Equipment Corporation, la VAX (Virtual Address eXtended) de la misma compañía, los modelos NOVA y ECLIPSE de Data General, la serie 3000 y 9000 de Hewlett - Packard con varios modelos el 36 y el 34, la Wang y Honey - Well -Bull, Siemens de origen alemán, la ICL fabricada en
Inglaterra. En la Unión Soviética se utilizó la US (Sistema Unificado, Ryad) que ha pasado por varias generaciones.
Cuarta Generación
Aquí aparecen los microprocesadores que es un gran adelanto de la microelectrónica, son circuitos integrados de alta
densidad y con una
velocidadimpresionante. Las microcomputadoras con base en estos circuitos son extremadamente pequeñas y baratas, por lo que su uso se extiende al mercado industrial. Aquí nacen las computadoras personales que han adquirido proporciones enormes y que han influido en la
sociedad en general sobre la llamada "
revolución informática".
En 1976 Steve Wozniak y Steve Jobs inventan la primera microcomputadora de uso masivo y más tarde forman la compañía conocida como la Apple que fue la segunda compañía más grande del mundo, antecedida tan solo por IBM; y esta por su parte es aún de las cinco compañías más grandes del mundo.
En 1981 se vendieron 800 00 computadoras personales, al siguiente subió a 1 400 000. Entre 1984 y 1987 se vendieron alrededor de 60 millones de computadoras personales, por lo que no queda duda que su impacto y penetración han sido enormes.
Con el surgimiento de las computadoras personales, el software y los sistemas que con ellas de manejan han tenido un considerable avance, porque han hecho más interactiva la comunicación con el usuario. Surgen otras aplicaciones como los procesadores de palabra, las hojas electrónicas de cálculo, paquetes
gráficos, etc. También las
industrias del Software de las computadoras personales crece con gran rapidez, Gary Kildall y William Gates se dedicaron durante años a la creación de sistemas operativos y
métodos para lograr una utilización sencilla de las microcomputadoras (son los creadores de CP/M y de los
productos de
Microsoft).
No todo son microcomputadoras, por su puesto, las minicomputadoras y los grandes sistemas continúan en desarrollo. De hecho las máquinas pequeñas rebasaban por mucho la capacidad de los grandes sistemas de 10 o 15 años antes, que requerían de instalaciones costosas y especiales, pero sería equivocado suponer que las grandes computadoras han desaparecido; por el contrario, su presencia era ya ineludible en prácticamente todas las esferas de control gubernamental, militar y de la gran
industria. Las enormes computadoras de las series CDC, CRAY, Hitachi o IBM por ejemplo, eran capaces de atender a varios cientos de millones de operaciones por segundo.
Quinta Generación
En vista de la acelerada marcha de la microelectrónica, la sociedad industrial se ha dado a la tarea de poner también a esa altura el desarrollo del software y los sistemas con que se manejan las computadoras. Surge la
competencia internacional por el
dominio del mercado de la
computación, en la que se perfilan dos líderes que, sin embargo, no han podido alcanzar el nivel que se desea: la capacidad de comunicarse con la computadora en un lenguaje más cotidiano y no a través de códigos o lenguajes de control especializados.
Japón lanzó en 1983 el llamado "programa de la quinta generación de computadoras", con los
objetivos explícitos de producir máquinas con innovaciones reales en los criterios mencionados. Y en los Estados Unidos ya está en actividad un programa en desarrollo que persigue objetivos semejantes, que pueden resumirse de la siguiente manera:
Procesamiento en paralelo mediante arquitecturas y diseños especiales y circuitos de gran velocidad.
Manejo de lenguaje natural y sistemas de
inteligencia artificial.
El futuro previsible de la computación es muy interesante, y se puede esperar que esta
ciencia siga siendo objeto de
atención prioritaria de gobiernos y de la sociedad en conjunto.
MODELO DE VON NEUMANN
Las computadoras digitales actuales se ajustan al modelo propuesto por el matemático John Von Neumann. De acuerdo con el, una característica importante de este modelo es que tanto los datos como los programas, se almacenan en la memoria antes de ser utilizados.
También se puede optar por utilizar los valores que presenta cada posición del número binario a ser transformado, comenzando de derecha a izquierda, y sumando los valores de las posiciones que tienen un 1.
entonces se suman los números 64, 16 y 2:
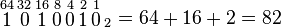Para cambiar de binario con decimales a decimal se hace exactamente igual, salvo que la posición cero (en la que el dos es elevado a la cero) es la que está a la izquierda de la coma y se cuenta hacia la derecha a partir de -1:
