Elblogdekevincito: El Sistema Binario

-El sistema binario, llamado también sistema diádico en ciencias de la computación, es un sistema de numeración en el que los números se representan utilizando solamente las cifras ceroy uno (0 y 1). Es uno de los que se utiliza en las computadoras, debido a que trabajan internamente con dos niveles de voltaje, por lo cual su sistema de numeración natural es el sistema binario (encendido 1, apagado 0).

Historia del sistema binario

Página del artículo Explication de l'Arithmétique Binaire de Leibniz.

El antiguo matemático indio Pingala presentó la primera descripción que se conoce de un sistema de numeración binario en el siglo tercero antes de nuestra era, lo cual coincidió con su descubrimiento del concepto del número cero.

Una serie completa de 8 trigramas y 64 hexagramas (análogos a 3 bits) y números binarios de 6 bits eran conocidos en la antigua China en el texto clásico del I Ching. Series similares de combinaciones binarias también han sido utilizadas en sistemas de adivinación tradicionales africanos, como el Ifá, así como en la geomancia medieval occidental.

Un arreglo binario ordenado de los hexagramas del I Ching, representando la secuencia decimal de 0 a 63, y un método para generar el mismo fue desarrollado por el erudito y filósofo Chino Adgart en el siglo XI.

En 1605 Francis Bacon habló de un sistema por el cual las letras del alfabeto podrían reducirse a secuencias de dígitos binarios, las cuales podrían ser codificadas como variaciones apenas visibles en la fuente de cualquier texto arbitrario.

El sistema binario moderno fue documentado en su totalidad por Leibniz, en el siglo XVII, en su artículo "Explication de l'Arithmétique Binaire". En él se mencionan los símbolos binarios usados por matemáticos chinos. Leibniz utilizó el 0 y el 1, al igual que el sistema de numeración binario actual.

En 1854, el matemático británico George Boole publicó un artículo que marcó un antes y un después, detallando un sistema de lógica que terminaría denominándose Álgebra de Boole. Dicho sistema desempeñaría un papel fundamental en el desarrollo del sistema binario actual, particularmente en el desarrollo de circuitos electrónicos.

Conversión entre binario y decimal

Decimal a binario

Se divide el número del sistema decimal entre 2, cuyo resultado entero se vuelve a dividir entre 2, y así sucesivamente hasta que el dividendo sea menor que el divisor, 2. Es decir, cuando el número a dividir sea 1 finaliza la división.
A continuación se ordenan los restos empezando desde el último al primero, simplemente se colocan en orden inverso a como aparecen en la división, se les da la vuelta. Éste será el número binario que buscamos.

Ejemplo: Transformar el número decimal 131 en binario. El método es muy simple:

131 dividido entre 2 da 65 y el residuo es igual a 1
 65 dividido entre 2 da 32 y el residuo es igual a 1
 32 dividido entre 2 da 16 y el residuo es igual a 0
 16 dividido entre 2 da 8  y el residuo es igual a 0                   
  8 dividido entre 2 da 4  y el residuo es igual a 0
  4 dividido entre 2 da 2  y el residuo es igual a 0
  2 dividido entre 2 da 1  y el residuo es igual a 0
  1 dividido entre 2 da 0  y el residuo es igual a 1
             -> Ordenamos los residuos, del último al primero: 10000011

En sistema binario, 131 se escribe 10000011

Ejemplo: Transformar el número decimal 100 en binario.

Otra forma de conversión consiste en un método parecido a la factorización en números primos. Es relativamente fácil dividir cualquier número entre 2. Este método consiste también en divisiones sucesivas. Dependiendo de si el número es par o impar, colocaremos un cero o un uno en la columna de la derecha. Si es impar, le restaremos uno y seguiremos dividiendo entre dos, hasta llegar a 1. Después sólo nos queda tomar el último resultado de la columna izquierda (que siempre será 1) y todos los de la columna de la derecha y ordenar los dígitos de abajo a arriba.

Ejemplo

100|0
 50|0
 25|1   --> 1, 25-1=24 y seguimos dividiendo entre 2
 12|0
  6|0
  3|1
  1|1   -->

Existe un último método denominado de distribución. Consiste en distribuir los unos necesarios entre las potencias sucesivas de 2 de modo que su suma resulte ser el número decimal a convertir. Sea por ejemplo el número 151, para el que se necesitarán las 8 primeras potencias de 2, ya que la siguiente, 2⁸=256, es superior al número a convertir. Se comienza poniendo un 1 en 128, por lo que aún faltarán 23, 151-128 = 23, para llegar al 151. Este valor se conseguirá distribuyendo unos entre las potencias cuya suma dé el resultado buscado y poniendo ceros en el resto. En el ejemplo resultan ser las potencias 4, 2, 1 y 0, esto es, 16, 4, 2 y 1, respectivamente.

Ejemplo

  2⁰=   1|0
  2¹=   2|0
  2²=   4|0
  2³=   8|0
  2⁴=  16|0
  2⁵=  32|0
  2⁶=  64|0
  2⁷= 128|1

Binario a decimal

Para realizar la conversión de binario a decimal, realice lo siguiente:

Inicie por el lado derecho del número en binario, cada cifra multiplíquela por 2 elevado a la potencia consecutiva (comenzando por la potencia 0, 2⁰).

Después de realizar cada una de las multiplicaciones, sume todas y el número resultante será el equivalente al sistema decimal.

Ejemplos:

(Los números de arriba indican la potencia a la que hay que elevar 2)

$\overset{5}{\mathop{1}}\,\overset{4}{\mathop{1}}\,\overset{3}{\mathop{0}}\,\overset{2}{\mathop{1}}\,\overset{1}{\mathop{0}}\,\overset{0}{\mathop{1}}\,_{2}=1\cdot 2^{5}+1\cdot 2^{4}+0\cdot 2^{3}+1\cdot 2^{2}+0\cdot 2^{1}+1\cdot 2^{0}=32+16+0+4+0+1=53$

$\overset{7}{\mathop{1}}\,\overset{6}{\mathop{0}}\,\overset{5}{\mathop{0}}\,\overset{4}{\mathop{1}}\,\overset{3}{\mathop{0}}\,\overset{2}{\mathop{1}}\,\overset{1}{\mathop{1}}\,\overset{0}{\mathop{1}}\,_{2}=1\cdot 2^{7}+0\cdot 2^{6}+0\cdot 2^{5}+1\cdot 2^{4}+0\cdot 2^{3}+1\cdot 2^{2}+1\cdot 2^{1}+1\cdot 2^{0}=128+0+0+16+0+4+2+1=151$

$\overset{5}{\mathop{1}}\,\overset{4}{\mathop{1}}\,\overset{3}{\mathop{0}}\,\overset{2}{\mathop{1}}\,\overset{1}{\mathop{1}}\,\overset{0}{\mathop{1}}\,_{2}=1\cdot 2^{5}+1\cdot 2^{4}+0\cdot 2^{3}+1\cdot 2^{2}+1\cdot 2^{1}+1\cdot 2^{0}=32+16+0+4+2+1=55$

También se puede optar por utilizar los valores que presenta cada posición del número binario a ser transformado, comenzando de derecha a izquierda, y sumando los valores de las posiciones que tienen un 1.

Ejemplo

El número binario 1010010 corresponde en decimal al 82. Se puede representar de la siguiente manera:

$\overset{64}{\mathop{1}}\,\overset{32}{\mathop{0}}\,\overset{16}{\mathop{1}}\,\overset{8}{\mathop{0}}\,\overset{4}{\mathop{0}}\,\overset{2}{\mathop{1}}\,\overset{1}{\mathop{0}}\,_{2}$

entonces se suman los números 64, 16 y 2:

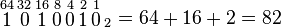$\overset{64}{\mathop{1}}\,\overset{32}{\mathop{0}}\,\overset{16}{\mathop{1}}\,\overset{8}{\mathop{0}}\,\overset{4}{\mathop{0}}\,\overset{2}{\mathop{1}}\,\overset{1}{\mathop{0}}\,_{2}=64+16+2=82$

Para cambiar de binario con decimales a decimal se hace exactamente igual, salvo que la posición cero (en la que el dos es elevado a la cero) es la que está a la izquierda de la coma y se cuenta hacia la derecha a partir de -1:

$\begin{align} & \overset{5}{\mathop{1}}\,\overset{4}{\mathop{1}}\,\overset{3}{\mathop{0}}\,\overset{2}{\mathop{1}}\,\overset{1}{\mathop{0}}\,\overset{0}{\mathop{1}}\,,\overset{-1}{\mathop{1}}\,\overset{-2}{\mathop{0}}\,\overset{-3}{\mathop{1}}\,=1\cdot 2^{5}+1\cdot 2^{4}+0\cdot 2^{3}+1\cdot 2^{2}+0\cdot 2^{1}+1\cdot 2^{0}+1\cdot 2^{-1}+0\cdot 2^{-2}+1\cdot 2^{-3}= \\ & =32+16+0+4+0+1+\frac{1}{2^{1}}+\frac{0}{2^{2}}+\frac{1}{2^{3}}=32+16+0+4+0+1+0,5+0+0,125=53,625 \\ \end{align}$

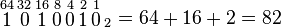
Operaciones con números binarios

Suma de números binarios

La tabla de sumar para números binarios es la siguiente:

+	0	1
0	0	1
1	1	10

Las posibles combinaciones al sumar dos bits son:

0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1 = 10

Note que al sumar 1 + 1 es 10₂, es decir, llevamos 1 a la siguiente posición de la izquierda (acarreo). Esto es equivalente en el sistema decimal a sumar 9 + 1, que da 10: cero en la posición que estamos sumando y un 1 de acarreo a la siguiente posición.

Ejemplo

        1
      10011000
    + 00010101
    ———————————
      10101101

Se puede convertir la operación binaria en una operación decimal, resolver la decimal, y después transformar el resultado en un (número) binario. Operamos como en el sistema decimal: comenzamos a sumar desde la derecha, en nuestro ejemplo, 1 + 1 = 10, entonces escribimos 0 en la fila del resultado y llevamos 1 (este "1" se llama acarreo o arrastre). A continuación se suma el acarreo a la siguiente columna: 1 + 0 + 0 = 1, y seguimos hasta terminar todas las columnas (exactamente como en decimal).

Resta de números binarios

El algoritmo de la resta en sistema binario es el mismo que en el sistema decimal. Pero conviene repasar la operación de restar en decimal para comprender la operación binaria, que es más sencilla. Los términos que intervienen en la resta se llaman minuendo, sustraendo y diferencia.

Las restas básicas 0 - 0, 1 - 0 y 1 - 1 son evidentes:

0 - 0 = 0
1 - 0 = 1
1 - 1 = 0
0 - 1 = 1 (se transforma en 10 - 1 = 1) (en sistema decimal equivale a 2 - 1 = 1)

La resta 0 - 1 se resuelve igual que en el sistema decimal, tomando una unidad prestada de la posición siguiente: 0 - 1 = 1 y me llevo 1 (este valor se resta al resultado que obtenga, entre el minuendo y el sustraendo de la siguiente columna), lo que equivale a decir en el sistema decimal, 2 - 1 = 1.

Ejemplos

        10001                           11011001    
       -01010                          -10101011
                                   
       ——————                          —————————
        00111                           00101110

En sistema decimal sería: 17 - 10 = 7 y 217 - 171 = 46.

Para simplificar las restas y reducir la posibilidad de cometer errores hay varios métodos:

Dividir los números largos en grupos. En el siguiente ejemplo, vemos cómo se divide una resta larga en tres restas cortas:

        100110011101             1001     1001     1101
       -010101110010            -0101    -0111    -0010
       —————————————      =     —————    —————    —————
        010000101011             0100     0010     1011

Utilizando el complemento a dos (C2). La resta de dos números binarios puede obtenerse sumando al minuendo el «complemento a dos» del sustraendo.

Ejemplo

La siguiente resta, 91 - 46 = 45, en binario es:

        1011011                                             1011011
       -0101110       el C2 de 0101110 es 1010010          +1010010
       ————————                                            ————————
        0101101                                            10101101

En el resultado nos sobra un bit, que se desborda por la izquierda. Pero, como el número resultante no puede ser más largo que el minuendo, el bit sobrante se desprecia.

Un último ejemplo: vamos a restar 219 - 23 = 196, directamente y utilizando el complemento a dos:

        11011011                                            11011011
       -00010111       el C2 de 00010111 es 11101001       +11101001
       —————————                                           —————————
        11000100                                           111000100

Y, despreciando el bit que se desborda por la izquierda, llegamos al resultado correcto: 11000100 en binario, 196 en decimal.

Utilizando el complemento a uno. La resta de dos números binarios puede obtenerse sumando al minuendo el complemento a uno del sustraendo y a su vez sumarle el bit que se desborda.

Fuente:

Wikipedia

Monografias.com

Elrincondelvago

Youtube

domingo, 30 de marzo de 2014

El Sistema Binario